This approximation again uses a simple spreadsheet, basic trigonometry and basic algebra to determine the correct electrostatic force between two spheres using the corrected equation derived above for the point to sphere force calculations.
For the purposes of this approximation the symmetry of a circle is used to approximate a sphere. Unit charge is also assumed for simplicity.
The illustration below demonstrates the approach of calculating the force between a sphere and a sphere by approximating a circle with many points, then simply summing the force between the point outside the circle and each of the many points on the circle using the corrected equation F_{e}=q_{1}q_{2}d/(d^2-r^2)^{3/2}) , not Coulomb’s Law, for the point to sphere force calculation.
Using a Cartesian plane to calculate the forces, Point 1, the centroid of Circle 1 lies outside the circle, the centroid of the circle is 0,0. Point 2 moves around the circle allowing many force calculations between Point 1 and Point 2 as Point 2 revolves around the circle using the corrected equation for the point to point force calculation (Point 1 is a sphere). Point 1 remains stationary.
Assuming 360 points on the circle, one for each degree, each point will have 1/360th of the charge of the entire circle. Forces in the Y direction are ignored as the corresponding point on the opposite side of the circle (across the X axis) exerts an equal and cancelling force in the Y direction.
The summed individual forces of the numerical approximation of a sphere to sphere do not equal the force calculated by Coulomb’s Law where two spheres are approximated as a points.
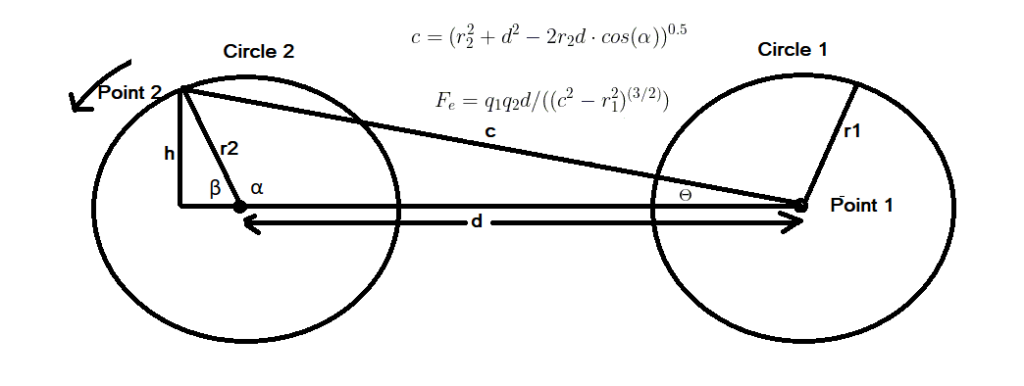
Note r_{1} is used in the force equation and used in the calculation of distance for the force.
Using the cosine law c=(r_{2}^2 + d^2 -2r_{2}d \cdot cos(\alpha))^{0.5}
The force along c is F_{e}=q_{1}q_{2}d/((c^{2}-r_{1}^{2})^{(3/2)})
Using basic trigonometry determine the X axis component of the force for each point as follows;
\beta =\pi-\alpha h=r_{2}\sin(\beta) \theta=a\sin(h/c)Resultant force along X axis = =F_{e} \cos(\theta))
Steps to reproduce point to sphere numerical force approximation using Coulomb’s Law in a spreadsheet;
For simplicity assume unit force on the point and the circle.
360 degrees are converted to rads purely to explain the concept in degrees.
Create a spreadsheet with nine columns;
| 1 | Degrees | Populate column one with the numbers 0 to 359 (one row for each degree) although this approximation is reproducible with as few as 11 rows. |
| 2 | Rads | The Rads column is the radian equivalent of degrees and in Excel this is =RADIANS() and simply the degrees in column 1 expressed as radians. |
| 3 | cos(α) | The cos(α) column is the cosine of the radians in the Rads column. |
| 4 | Separation distance c | Determine the separation distance from the rotating point to the centroid of Circle 1 c=(r_{2}^2 + d^2 -2r_{2}d \cdot cos(\alpha))^{0.5} as alpha increases, moving point 2 around Circle 1, one degree at a time. |
| 5 | β | π –α |
| 6 | h | r2 sin(β) |
| 7 | θ | = asin(h/c) |
| 8 | Corrected force calculation | F_{e}=q_{1}q_{2}d/((c^{2}-r_{1}^{2})^{(3/2)}) |
| 9 | Force along X axis | Fe cos(θ) |
Summing column nine gives the total force between the two spheres using the corrected equation in a numerical approximation.
A sample spreadsheet table is below. The full table is in Appendix 3.
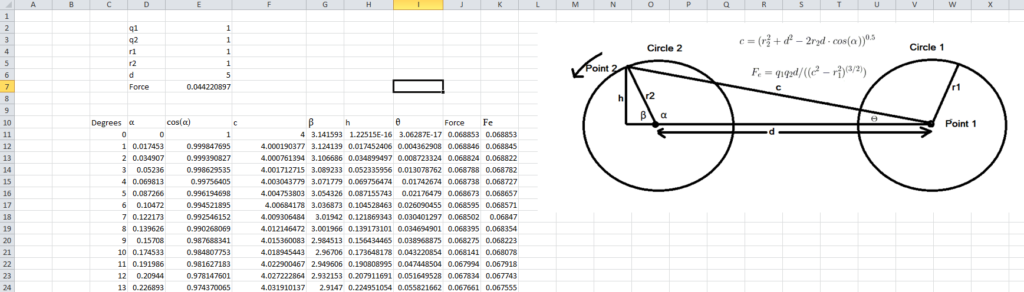
Results;
- Using unit charge on both spheres, with a radius of 1 and a distance of 5r the numerical approximation yields a force of k0.044220897 N. Coulomb’s Law, treating the circle as a point, yields a force of 0.04. Increasing the number of points on the circle improves the precision of the result but a difference remains.
- The numerical approximation produces a force between two spheres that is different from the previous force calculation between a point and a sphere.