For the purposes of this exercise the symmetry of a circle is used to approximate a sphere.
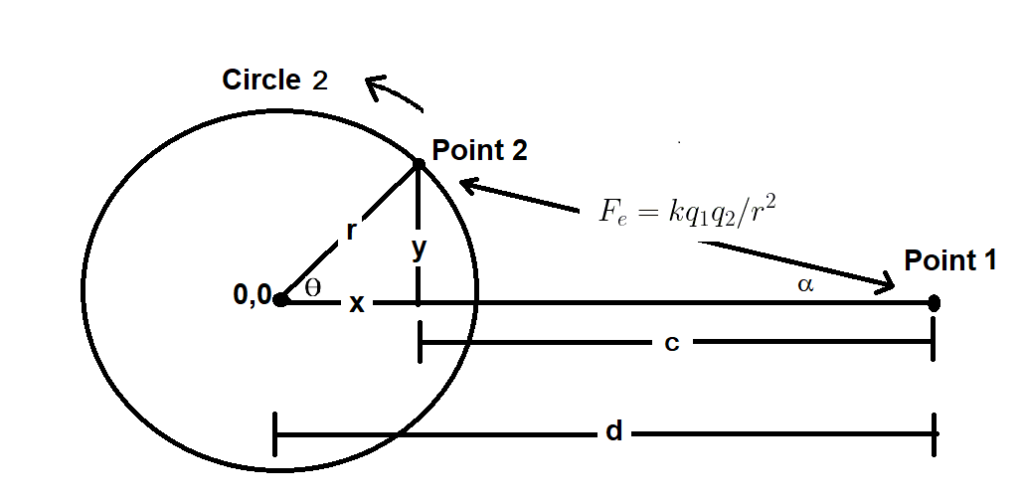
Figure 3 below demonstrates the approach of calculating the force between a point and a sphere by approximating a circle with many points, then simply summing the force between the point outside the circle and each of the many points on the circle using Coulomb’s Law: F_{e}=kq_{1}q_{2}d/r^{2} . Using a Cartesian plane to calculate the forces, Point 1 lies outside the circle, the centroid of the circle is 0,0. Point 2 moves around the circle allowing many force calculations between Point 1 and Point 2 as Point 2 revolves around the circle. Point 1 remains stationary.
Assuming 360 points on the circle, one for each degree, each point will have 1/360th of the charge of the entire circle. Forces in the Y direction are ignored as the corresponding point on the opposite side of the circle (across the X axis) exerts an equal and cancelling force in the Y direction.
The individual forces summed in the numerical approximation do not equal the force calculated by Coulomb’s Law where the sphere is approximated as a single point.
Figure 3 – Cartesian Coordinates Used for Numerical Approximation of point to sphere forces using Coulomb’s Law
Steps to reproduce point to sphere numerical force approximation using Coulomb’s Law in a spreadsheet;
- For simplicity assume unit force on the point and the circle.
- Degrees are converted to rads purely to explain the concept in degrees.
- Create a spreadsheet with six columns;
| Columns in the Spreadsheet | Title of the Column | Explanation of the calculation in the column |
|---|---|---|
| 1 | Degrees | Populate column one with the numbers 0 to 359 (one row for each degree in a circle) although this approximation is reproducible with as few as 11 rows. |
| 2 | Rads | The Rads column is the radian equivalent of degrees and in Excel this is =RADIANS() and simply the degrees in column 1 expressed as radians. |
| 3 | \cos (\theta) | The \cos (\theta) column is the cosine of the radians in the Rads column. |
| 4 | Separation distance c = d-x=d-r cos(\theta)) | Determine the separation distance along the X axis as c. c = d-x=d-r cos(\theta)) as theta increases, moving point 2 around the circle, one degree at a time. |
| 5 | Coulomb’s Law force calculation F_{e}=1/c^{2} | Assuming unit charge for the point and the circle. F_{e}=1/c^{2} is the inverse of column 4 squared, or the Coulombic Law for that point to point interaction. |
| 6 | Net point force (1/360)*1/c^2) | Column six is the force calculation using Coulomb’s Law for the point outside the circle to the point on the circle. Force in the x direction between Point 1 and the point on the circle is (1/360)*1/c^2) as point 2 moves around the circle where 360 is the number of points on the circle. |
Summing column six gives the total force between the circle and the point outside the circle using Coulomb’s Law in a numerical approximation of a point to a sphere.
A sample spreadsheet table is below. The full table is in Appendix 2.
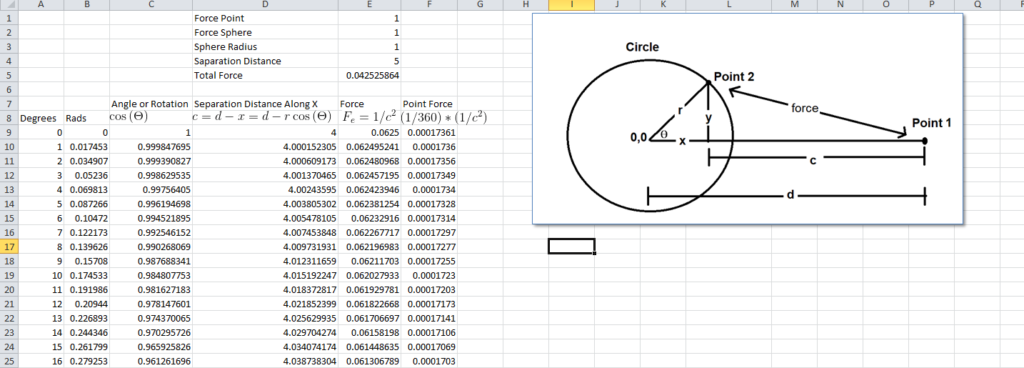
Figure 4 – Spreadsheet numerical approximation of point to sphere force calculation.
Results;
- Using unit charge on both the point outside the circle and on the circle itself, with a unit circle radius and a distance of 5r the spreadsheet numerical approximation yields a force of k0.042525864 N. Treating the circle conventionally as a point yields a force of k0.040000 N. Increasing the number of points on the circle improves the precision of the result but a difference remains.
- Differences between Coulomb’s Law and the numerical approximation remain regardless of the radius of the circle or distance between the circle and the point, with the obvious exception of a zero radius circle. In the case of a zero radius circle the numerical approximation matches Coulomb’s Law – a circle of zero radius is a point.