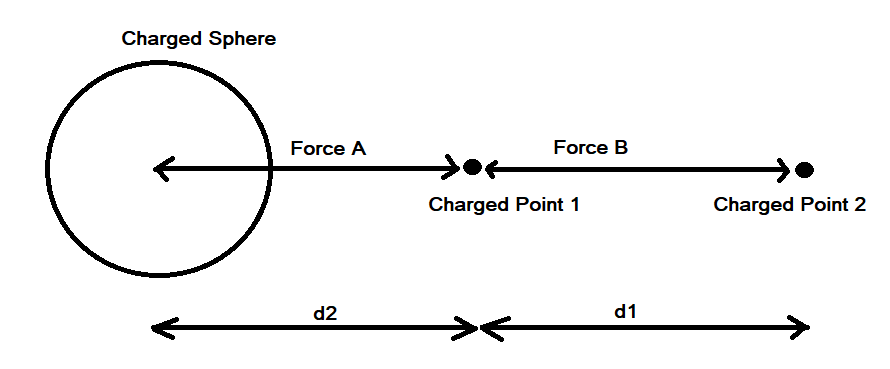
Contemporary thinking [1] holds that the calculation to determine electrostatic force between a point and a sphere is approximated as the force between a point and a point; the sphere is approximated as a point. A simple numerical approximation of a point to sphere interaction using Coulomb’s Law in a spreadsheet shows that the conventional approximation of a point to sphere interaction as a point to point interaction is incorrect. The force between a point and a sphere does not equal the force between a similarly charged point and another point at equivalent distance.
This paper evolves an equation that correctly determines electrostatic force between a point and a sphere and investigates applications of the corrected equation. Given that molecules are effectively charged points interacting with charged spheres, a substantial new electrostatic force at the molecular level is a disruptive concept with profound implications.
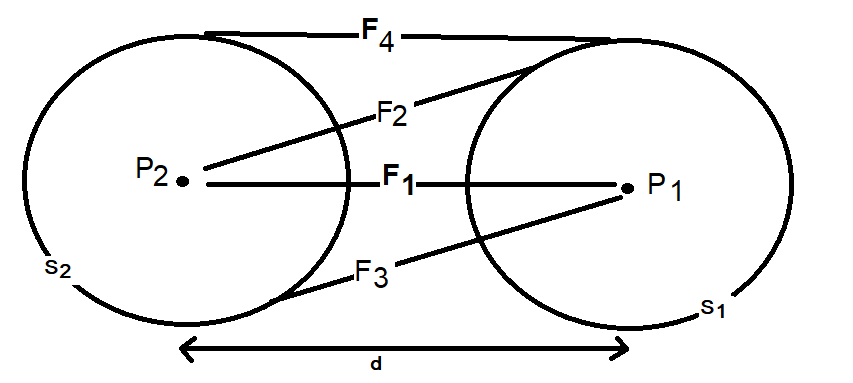
The incorrect point to point approximation yields zero net electrostatic force between two Hydrogen atoms at any distance. This paper proceeds to calculate and sum the four forces (F1 to F4) in Figure 2 using the corrected equation to determine the net force at various distances (d) between two Hydrogen atoms.
Using a Hydrogen radius of 53pm the corrected point to sphere calculation yields a net electrostatic force that varies over distance forming a Lennard Jones curve[2] predicting a stable nuclear separation distance of 170pm[3]. The same corrected equation also produces an electrostatic force larger than gravity at great distance[4]. Elements larger than Hydrogen and more complex electron probability distributions were not investigated. The proton is considered a point force throughout this paper despite having volume. The gravity calculations are not possible using a normal version of Excel due to the level of precision required. Precision greater than 65 digits is required to calculate gravity at 1m. A simple HTML web page using JavaScript with extended precision libraries was used to calculate force at great distances. The JavaScript also simplifies repeating the force calculations over many distance intervals. All spreadsheets and JavaScript are attached as appendices. The HTML page that executes the JavaScript accepts parameters of varying radii, charges and separation distance.
This paper requires only a basic understanding of trigonometry, basic algebra and the ability to enter formulae into a spreadsheet. An understanding of calculus is not required but may help follow the derivation of the correct equation. An understanding of JavaScript is only required to follow the iterative process of executing the same force equations repeatedly for purposes of simplifying the graphing forces over distance involving numerical approximations.
[1] See Appendix 1 for a list of web sites that approximate point to sphere force calculations as point to point force calculations
[3]A radius of 25 pm produces a separation distance of 81pm.
[4] See Section 8. Using 70 decimal places of precision the corrected equation presents a force of 4.8e-49N at 1m. The expected result is 1.8e-64N.